齒輪所產生的噪音 - 不見、不聞、不言
.png)
| 你可能會記得三不猴的故事,他們不見惡事、不聽惡詞、不說惡言。 人們常常在尋找齒輪噪音的原因時想起這件事。 齒輪品質的評估並不缺乏標準,許多製造商已經投入於研發專利量測方法, 來評估幾何特徵及其他特徵。 但是什麽幾何特徵與齒輪噪音有相關性呢? |
.png)
不聞齒輪噪音
雖然可透過量測儀器看出所有事物,但是齒輪的噪音卻無法透過儀器來進行判別。每個品管經理都希望齒輪「越精確越好」。但是,有時後愈精確似乎不一定愈好。自從工程師開始關注齒輪傳動時的噪音,他們發現品質高的齒輪所產生的噪音未必較小。因此,對於許多製造經理來說,每天的挑戰都是在生產線尾端的測試台上,某些層面上來看就像唐吉訶德與風車的決鬥。有時候甚至發現高精度齒輪的變速器比一般齒輪產生更多噪音。這是為什麼?
齒輪噪音是齒的接觸而產生。而齒的接觸是由齒面的形狀決定的,人們可以根據齒面的幾何形狀來預測齒輪的噪聲。但經驗告訴我們,傳統的齒輪測量儀器適用於控制生產製程,但並不能準確地預測噪音。然而許多地方的齒面和齒輪的幾何公差正在不斷縮小,期望更精確的幾何形狀能夠改善噪音的問題。
本文將探討噪音分析的主題,以更深入的了解齒輪噪音。沒有人會質疑齒輪的接觸是噪音的來源。因此,我們必須找出是什麼原因導致了齒輪的旋轉傳動誤差,並尋找客觀描述實際旋轉傳動特性的方法,同時了解噪音的原因, 即使它們可能很小。
.png)
齒輪設計:傳動誤差分析
齒面相對修形是傘齒輪組設計的核心。對於設計工程師來說,一對相互嚙合的齒面之間、無傳輸誤差的最小距離是意義甚大的(見圖1 )透過檢查齒面相對修整,人們可以立刻識別齒面輪廓的修整,對Gear(大傘 )及Pinion(小傘)之問,生產相關或是負載相關所造成的位移敏感度有初步的了解。而齒面相對修整也適用於齒面接觸分析和計算理論傳動誤差。
根據齒面相對修整,一對傘齒輪的傳動誤差可以很容易計算出來。對於Gear(大傘)和Pinion(小傘)的每個角度位置,齒面彼此之問都有特定的距
離。
.png)
圖 2 : 接觸路徑、個別齒輪接觸、多齒輪接觸與傳動誤差
| 如果我們轉動Gear(大傘)直到與 Pinion(小傘)齒面接觸,互相嚙合的齒面就會恰好在一個點上接觸。這個接觸點是因為齒輪側面凸起。如果我們使接觸距離為零,側面會在一條線上彼此接觸,這稱為共軛齒輪傳動。 所有接觸點所在之處稱為接觸路徑。因為接觸路徑上的每個點也與Pinion(小傘)角度具有關聯, 所以可以透過節距來確定齒輪組的嚙合開始到嚙合結束。 如果我們將齒面上的接觸路徑投影到齒面相對修整,齒面相對修整中接觸路徑上的該點距離就是這個角度位置的傳輸誤差(參見圖2)。對於常規設計的齒輪, 我們獲得了齒輪的拋物線傳動誤差。 所有傳輸誤差曲線可透過複製一個齒輪組的傳動誤差曲線並將其移動一個齒距來獲得。下一對齒輪的傳動誤差在單一個接合開始和結束的點與當前傳動誤差曲線相交。因此,我們得到圖2所示的曲線作為傘齒輪的無負載傳動誤差。 |
階次分析
根據齒面的設計,這種傳動誤差可能較高、較尖、較寬或較短。這樣的屬性不適合讓傳動誤差曲線以量化表示。
.png)
圖 3 : 階次分析與傳動誤差曲線
.png)
不見傳動誤差原因
在一個簡單的測試中,我們利用階次分析擭得齒輪規律轉動和傳動誤差的資料,代表我們可以「聽見」齒輪傳動誤差,但仍舊無法看出其背後原因。
多年來,階次分析已成為描述週期性功能的方式。階次分析是基於傅立葉轉換,在法國數學家約瑟夫·傅立葉(Joseph Fourier) 的著作中提出 , 每個週期函數都可以分解為不同相位,振幅和頻率的諧波正弦振盪(見圖3)
藍色曲線是齒對的傳動誤差曲線。第一步是找到與齒輪網格長度相對應的波長的正弦曲線。應選擇適當的幅度和相位,以確保正弦曲線盡可能接近藍色曲線。這個正弦曲線的幅度稱為第一階次。每個後續步驟在前一步驟中尋找具有曲線波長的一半的正弦曲線, 使得所有先前正弦曲線的總和盡可能接近藍色傳動誤差曲線。這裡的每個幅度都稱為一個階次。如圖3所示,累積曲線顯示為紅色虛線。如上所述,傅立葉提出以下理論:每個週期性曲線(傳動誤差是這樣的曲線)可以精確地描述為具有越來越短的波長的無限正弦曲線。
這個原理被用來描述傳動誤差曲線的階次的大小,真中n階對應到波長1/n的正弦函數的幅度。因此,我們找到了一個適合的數學工具來描述傳動誤差曲線
在車輛聲音工程領域中,另一個參考文獻已經也成為一種可接受的描述齒輪組傳動誤差的方式: Pinion(小傘)的旋轉被當作參考基準,取代只用齒輪的接觸順序。例如,如果我們有一個15齒的 Pinion(小傘),當使用這個參考基準時,第一個齒接觸順序變成 Pinion(小傘)的15階。
很重要的一點是,透過對傳動誤差曲線,在階譜中只能出現整數倍的齒數。由於傅力葉分析的基礎是從階到階的半波長正弦函數, 因此永遠不會發生不能被齒數整除的階次。
多年來,階次分析已成為描述週期性功能的方式。階次分析是基於傅立葉轉換,在法國數學家約瑟夫·傅立葉(Joseph Fourier) 的著作中提出 , 每個週期函數都可以分解為不同相位,振幅和頻率的諧波正弦振盪(見圖3)
藍色曲線是齒對的傳動誤差曲線。第一步是找到與齒輪網格長度相對應的波長的正弦曲線。應選擇適當的幅度和相位,以確保正弦曲線盡可能接近藍色曲線。這個正弦曲線的幅度稱為第一階次。每個後續步驟在前一步驟中尋找具有曲線波長的一半的正弦曲線, 使得所有先前正弦曲線的總和盡可能接近藍色傳動誤差曲線。這裡的每個幅度都稱為一個階次。如圖3所示,累積曲線顯示為紅色虛線。如上所述,傅立葉提出以下理論:每個週期性曲線(傳動誤差是這樣的曲線)可以精確地描述為具有越來越短的波長的無限正弦曲線。
這個原理被用來描述傳動誤差曲線的階次的大小,真中n階對應到波長1/n的正弦函數的幅度。因此,我們找到了一個適合的數學工具來描述傳動誤差曲線
在車輛聲音工程領域中,另一個參考文獻已經也成為一種可接受的描述齒輪組傳動誤差的方式: Pinion(小傘)的旋轉被當作參考基準,取代只用齒輪的接觸順序。例如,如果我們有一個15齒的 Pinion(小傘),當使用這個參考基準時,第一個齒接觸順序變成 Pinion(小傘)的15階。
很重要的一點是,透過對傳動誤差曲線,在階譜中只能出現整數倍的齒數。由於傅力葉分析的基礎是從階到階的半波長正弦函數, 因此永遠不會發生不能被齒數整除的階次。
製造誤差:不精確
但我們仍然處於齒輪設計的美妙世界,而且不知道製造的不準確性會大大改變齒到齒的傳動誤差曲線。.png) 圖4: 徑向跳動的傳動誤差曲線
圖4: 徑向跳動的傳動誤差曲線.png)
圖5: 徑向跳動與雙擊
.png)
圖6: 間距誤差
圖4為徑向跳動發生時的傳動誤差曲線。如圖2所示,單一個齒輪網格不再直線排列,相反的,它們沿著正弦波被“串起來”。某些齒輪組只會產生較短的且不明顯的傳對誤差;某些會有更長的齒面接觸與更大的誤差,如紅色曲線所示。這被稱為幅度調變和頻率調變;在階次分析中,這可以被看作是邊帶。偏心本身就出現在小齒輪的第一階。
如果徑向跳動不是一個簡單的正弦波,額外的邊帶出現在齒輪接觸的階次旁(見圖5)。除了徑向跳動外,還出現了”雙擊”現象。
另一個影響表現為分度誤差。在這種情況下,會逐漸減少階次而不是邊帶(參見圖6)。這種螺距誤差可能發生在傘齒輪或剖面磨削的圓柱齒輪中。由於砂輪的磨損,使得齒輪的齒不斷得變厚。在從第一個到最後一個齒隙的轉換過程中可能會出現較大的分度誤差。這在階譜中,可由多個階次證明,而不是由邊帶證明。
幽靈階次
每一個不能被齒數整除的階次都被稱為幽靈階次一 因為沒有一個更好的術語。幽靈階次在噪音分析時受到特別關注,因為它們不會受到齒輪幾何形狀的替代設計的影響。.png)
圖7 : 齒輪接觸的順序與幽靈階次
.png)
不說惡言猴
我們該如何讓可以看、聽的第三隻猴子說話呢?相反的,他們似乎像一個幽靈,是各種製造不準確的結果。
圖7顯示出在小齒輪處具有15齒傳動裝置的測量傳動誤差曲線。一些齒接觸階次可以清楚地看出為第15,30,45,60,85,90和105階。但是在這之間還有很多其他的幽靈階次,由於發生原因不明,難以在優化傳動噪音時進行控制。
不說惡言猴說話了一我們必須了解牠
三隻猴子的故事精準的描述了測量技術、進行測試與噪音來源三者間的矛盾。為了讓第三隻猴子說話,我們須找到產生讓人感覺到如此不愉快的噪聲的幾何特徵。
圓柱齒輪的測量原理
如果我們考慮一個圓柱齒輪的齒形測量值,我們可以確定幾項影響原因:存在幾何誤差,例如齒形角誤差,不完美的隆齒或不正確的倒角。只有在消除了宏觀幾何誤差時,齒面上的表面缺陷才可見。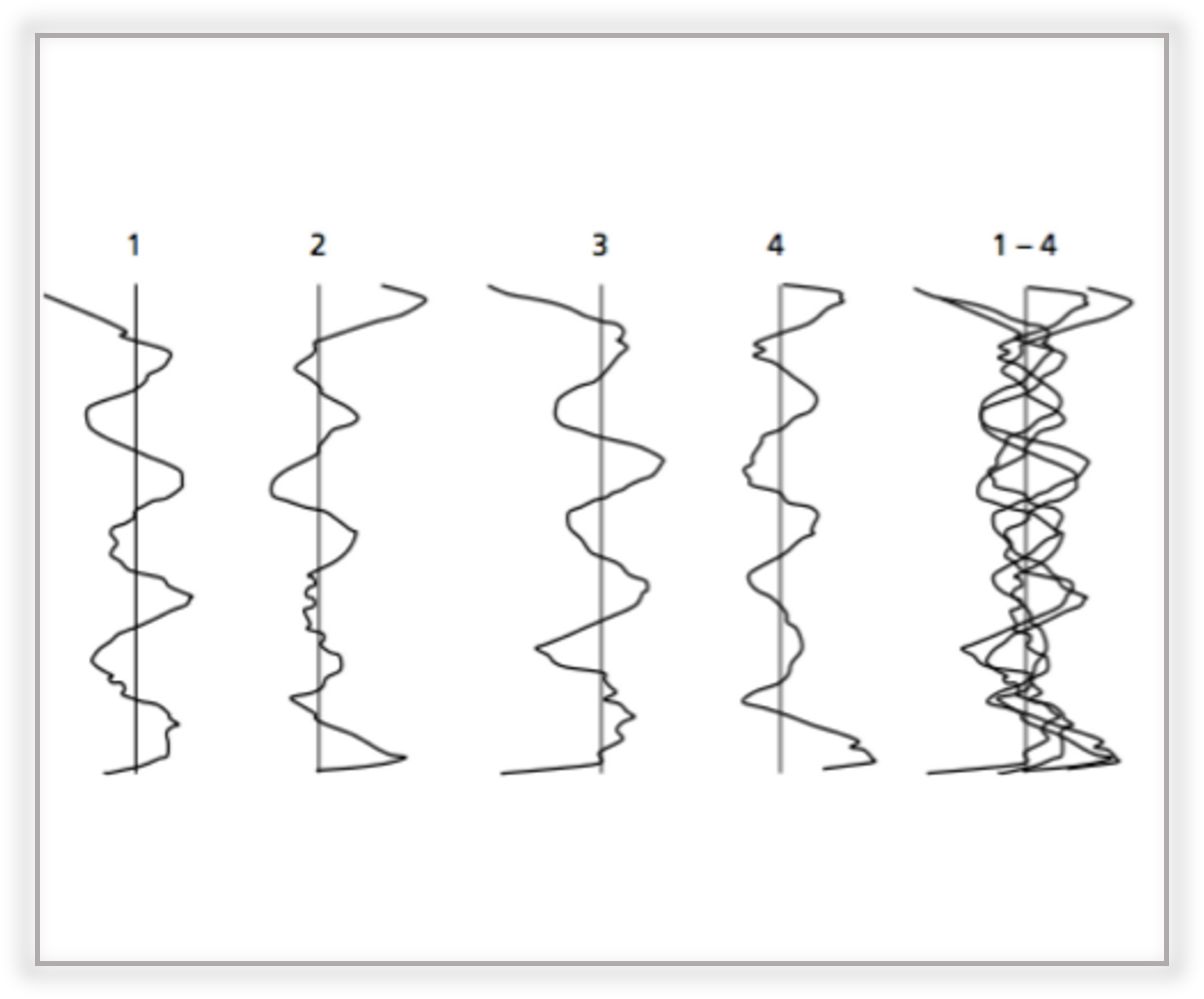
圖8: 齒形測量結果
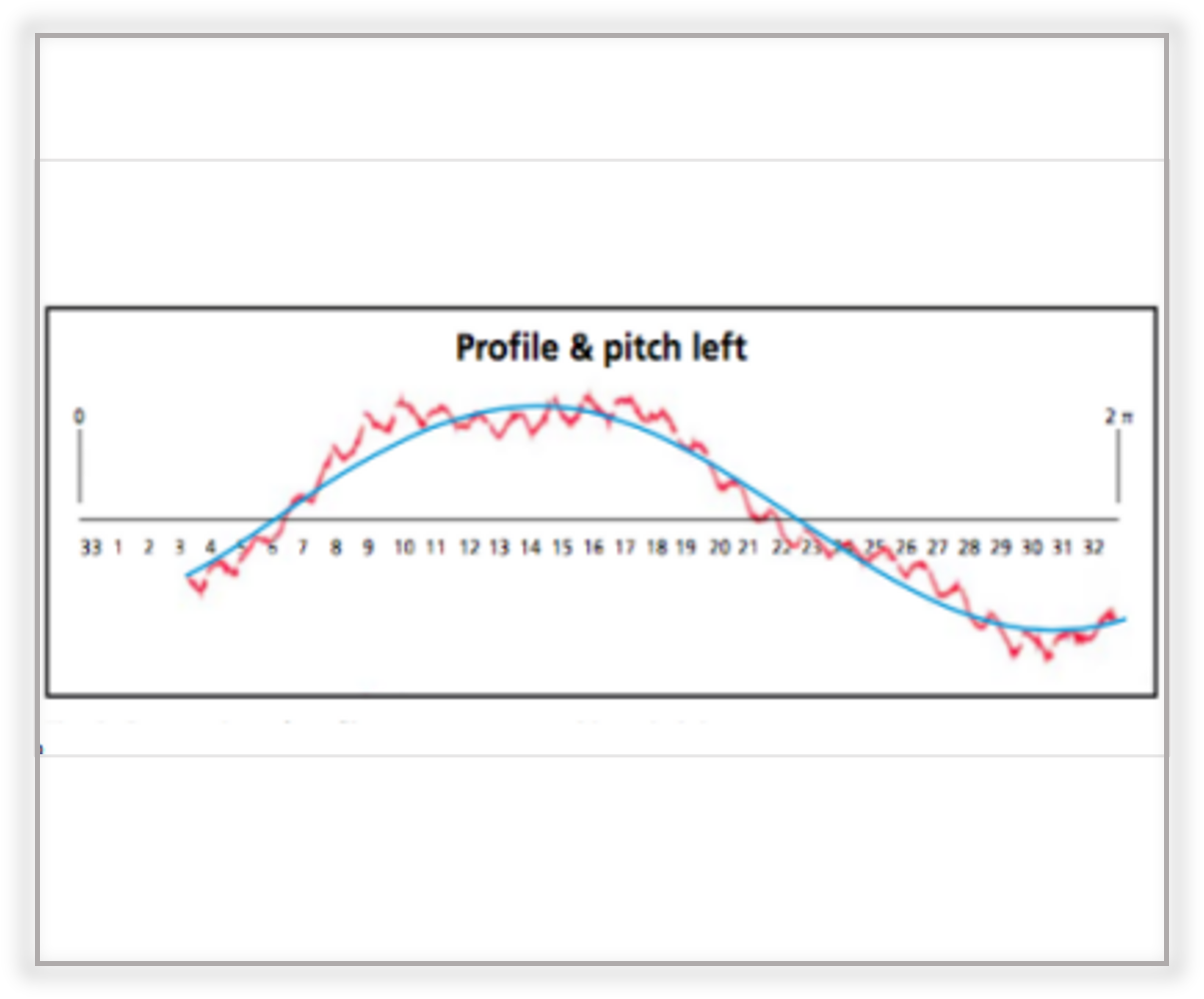
圖9:齒形測量順序
.png)
圖10 : 次序的階次分析
圖8顯示了從幾何誤差取出的齒形測量結果。如果我們疊加所有的齒形測量,如右側的部分所示,即使專業的人員也看不出任何東西。
有人可能會假設在這裡可以看到齒面的粗糙度。但是這個假設會導致錯誤的結果。
在未修正齒跡的直齒輪傳動,無負載交互齒面在平行於齒根的直線上相互觸。對於元件的每個旋轉角度,產生不同的接觸線。如果我們現在添加節距測量值, 則可以為齒形測量上的每個點的所有齒分配齒輪的旋轉角度。如果我們沿旋轉角度和節距測量來排列所有齒形測量結果,則我們獲得圖9中所示的曲線。
有人可能會假設在這裡可以看到齒面的粗糙度。但是這個假設會導致錯誤的結果。
在未修正齒跡的直齒輪傳動,無負載交互齒面在平行於齒根的直線上相互觸。對於元件的每個旋轉角度,產生不同的接觸線。如果我們現在添加節距測量值, 則可以為齒形測量上的每個點的所有齒分配齒輪的旋轉角度。如果我們沿旋轉角度和節距測量來排列所有齒形測量結果,則我們獲得圖9中所示的曲線。
之前看起來不平整的表面粗糙度現在規則的顯示在齒面上。藍線是由齒輪加工時的徑向跳動產生的。正如我們由過去經驗所學到的,這不是噪音大的原因。齒面上的波紋在圖9中清晰可見,由此可知齒輪中的令人不快的噪音是由這種波紋引起的。
如果我們應用上面介紹的階次分析方法來描述所有齒形測量的階次,我們可以獲得關鍵資訊來解釋噪音。
慢慢地,但是肯定的是,我們的第三隻猴子開始說話!
如果我們應用上面介紹的階次分析方法來描述所有齒形測量的階次,我們可以獲得關鍵資訊來解釋噪音。
慢慢地,但是肯定的是,我們的第三隻猴子開始說話!
圖10顯示了從宏觀幾何誤差的齒形測量值取出的階次分析。來自齒輪加工的徑向跳動在第一階清晰可見。緊接著是二三號的小階次。第四階又顯示更高的幅度,這值得仔細注意。圖10顯示了階譜下的完整序列,在其下方顯示序列減去一階,二階和三階。一個不尋常的四重打擊疊加在波紋上。
這種效應背後的原因是在齒面加工之前就已經存在了:用於加工該齒輪的轉動元件的鍛造部分如果來自鍛造成圓形的矩形鑄件。在熱處理過程中,材料就會記住原來的矩形形狀,這會導致硬化變形,產生這種四重打擊。
如果我們從階次中去掉1到4階, 我們可以得到圖10中下半部的圖。我們可以很容易地看出一個明顯的第二十八階波紋。事實上,這也是噪音問題的根源,它干擾齒輪磨合測試。因為這個組件有33 個齒,第二十八階波紋是一個幽靈階次,我們現在必須了解它的原因。齒輪幾何的最佳化只能影響可被齒數整除的階次,因此無法解決這個現象。
因此,這是來自齒輪加工時發生的故障。在很多情況下,機床是個問題。值得注意的是,這種波紋的幅度非常小,我們看到的幅度小於1微米。
這是由機床週期性的不規則造成的。例如主軸軸承可能因為磨損失去了原來的完美同心度。有時,直接驅動的電子控制參數的校準不完美也可能是關鍵因素。如果直接驅動裝置有許多對應於階次的極對,通常是問題的根源。
除了與機器相關的原因之外,機床周圍還有其他的影響。例如,位於同一工廠內的機器可能讓地板振動一並且這種振動在某些情況下可以傳遞給齒輪加工機器。但我們正在尋找小於1微米的振幅。
圖10中的下一個異常是第33階。這並不奇怪,因為齒輪有33個齒如果我們想要最小化這個順序,我們必須利用齒輪最佳化。
這種效應背後的原因是在齒面加工之前就已經存在了:用於加工該齒輪的轉動元件的鍛造部分如果來自鍛造成圓形的矩形鑄件。在熱處理過程中,材料就會記住原來的矩形形狀,這會導致硬化變形,產生這種四重打擊。
如果我們從階次中去掉1到4階, 我們可以得到圖10中下半部的圖。我們可以很容易地看出一個明顯的第二十八階波紋。事實上,這也是噪音問題的根源,它干擾齒輪磨合測試。因為這個組件有33 個齒,第二十八階波紋是一個幽靈階次,我們現在必須了解它的原因。齒輪幾何的最佳化只能影響可被齒數整除的階次,因此無法解決這個現象。
因此,這是來自齒輪加工時發生的故障。在很多情況下,機床是個問題。值得注意的是,這種波紋的幅度非常小,我們看到的幅度小於1微米。
這是由機床週期性的不規則造成的。例如主軸軸承可能因為磨損失去了原來的完美同心度。有時,直接驅動的電子控制參數的校準不完美也可能是關鍵因素。如果直接驅動裝置有許多對應於階次的極對,通常是問題的根源。
除了與機器相關的原因之外,機床周圍還有其他的影響。例如,位於同一工廠內的機器可能讓地板振動一並且這種振動在某些情況下可以傳遞給齒輪加工機器。但我們正在尋找小於1微米的振幅。
圖10中的下一個異常是第33階。這並不奇怪,因為齒輪有33個齒如果我們想要最小化這個順序,我們必須利用齒輪最佳化。
傘齒輪的測量原理
對於圓柱齒輪,通過齒形測量的智慧排序可以理解齒輪的階次。對於傘齒輪也同樣可行,如果對接觸路徑進行量和評估,來取代齒形測量。實務經驗:第三張量表
雖然這種評估測量結果的新方法與噪音行為確實有相關,但它有一個關鍵的缺點:必須在每個齒上測量圓柱齒輪齒形或傘齒輪接觸路徑。這個耗時的方式很難在日常操作中應用波紋度分析。對於正常生產過程中的品質控制不用對每個齒輪的齒進行測量就可以獲得夠好的結果。那麼評估就是基於這個測量的結果。這當然不能讓我們找到噪音的原因,但它可以使我們能夠確定齒輪是否會產生噪音。
|
測量的新方法
與噪音的來源有相關性
|
第三張量表顯示了圖11中紅色的無宏觀幾何誤差的齒形測量,對於每個剖面測量,其階次分析會顯示在藍色欄旁邊。
這裡顯示的階次不能得出關於波紋起因的任何結論,他們只能表明波紋存在。用戶可以選擇在階次曲線上疊加公差帶。如果其中一個階次超出了公差範圍,則以紅色突出顯示。
.png)
圖11 : 第三張量表
.png)
總結
就像猴子的比喻,在齒輪測量和測試中常常缺乏評估齒輪噪音的關鍵能力:齒輪測量非常適用於齒輪的幾何檢測,可以在較小的誤差範圍內精確地控制生產。但傳統的齒輪測量不適合預測噪音特徵一就像一隻看見但聽不到邪惡的猴子。進行測試是完全不同的事,它非常適合於評估齒輪對中的噪音。但噪音來自哪裡仍是無法確定。甚至不可能將噪音或其部分歸因於兩個相互嗤合的齒輪之一- 一個聽得到卻看不到邪惡的猴子。
我們如何成功找到引起噪音的幾何特徵,並在齒輪測試過程中也可以進行測量?有一種方法可以給第三隻猴子一個聲音。傅立葉階次分析為此提供了基本的數學框架。它使我們能夠找到亞微米範圍內的波紋並將其歸因於各種因素。當然,我們的猴子還是不能說標準的“齒輪英語”,但透過一點點努力,我們可以很容易地理解他……
